ZonoOpt::HybZono Class Reference

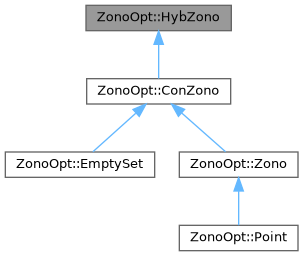
Hybrid zonotope class. More...

#include <HybZono.hpp>

Inheritance diagram for ZonoOpt::HybZono:

Public Member Functions
	HybZono ()=default
	Default constructor for HybZono class.
	HybZono (const Eigen::SparseMatrix< zono_float > &Gc, const Eigen::SparseMatrix< zono_float > &Gb, const Eigen::Vector< zono_float, -1 > &c, const Eigen::SparseMatrix< zono_float > &Ac, const Eigen::SparseMatrix< zono_float > &Ab, const Eigen::Vector< zono_float, -1 > &b, bool zero_one_form=false, bool sharp=false)
	HybZono constructor.
virtual	~HybZono ()=default
void	set (const Eigen::SparseMatrix< zono_float > &Gc, const Eigen::SparseMatrix< zono_float > &Gb, const Eigen::Vector< zono_float, -1 > &c, const Eigen::SparseMatrix< zono_float > &Ac, const Eigen::SparseMatrix< zono_float > &Ab, const Eigen::Vector< zono_float, -1 > &b, bool zero_one_form=false, bool sharp=false)
	Reset hybrid zonotope object with the given parameters.
virtual HybZono *	clone () const
	Clone method for polymorphic behavior.
virtual int	get_n () const
	Returns dimension of set.
virtual int	get_nC () const
	Returns number of constraints in set definition.
virtual int	get_nG () const
	Returns number of generators in set definition.
virtual int	get_nGc () const
	Returns number of continuous generators in set definition.
virtual int	get_nGb () const
	Returns number of binary generators in set definition.
virtual Eigen::SparseMatrix< zono_float >	get_Gc () const
	Returns continuous generator matrix.
virtual Eigen::SparseMatrix< zono_float >	get_Gb () const
	Returns binary generator matrix.
virtual Eigen::SparseMatrix< zono_float >	get_G () const
	Returns generator matrix.
virtual Eigen::SparseMatrix< zono_float >	get_Ac () const
	Returns continuous constraint matrix.
virtual Eigen::SparseMatrix< zono_float >	get_Ab () const
	Returns binary constraint matrix.
virtual Eigen::SparseMatrix< zono_float >	get_A () const
	Returns constraint matrix.
virtual Eigen::Vector< zono_float, -1 >	get_c () const
	Returns center vector.
virtual Eigen::Vector< zono_float, -1 >	get_b () const
	Returns constraint vector.
virtual bool	is_0_1_form () const
	Returns true if factors are in range [0,1], false if they are in range [-1,1].
bool	is_sharp () const
	Returns true if set is known to be sharp.
virtual void	convert_form ()
	Converts the set representation between -1-1 and 0-1 forms.
virtual void	remove_redundancy (int contractor_iter=100)
	Removes redundant constraints and any unused generators.
virtual std::unique_ptr< ConZono >	convex_relaxation () const
	Returns convex relaxation of the hybrid zonotope.
virtual std::unique_ptr< HybZono >	complement (const zono_float delta_m=100, const bool remove_redundancy=true, const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr, const int n_leaves=std::numeric_limits< int >::max(), const int contractor_iter=100)
	Computes the complement of the set Z.
bool	is_point () const
	Polymorphic type checking: true if set is a point.
bool	is_zono () const
	Polymorphic type checking: true if set is a zonotope.
bool	is_conzono () const
	Polymorphic type checking: true if set is a constrained zonotope.
bool	is_hybzono () const
	Polymorphic type checking: true if set is a hybrid zonotope.
bool	is_empty_set () const
	Polymorphic type checking: true if set is empty set object.
virtual std::string	print () const
	Returns set information as a string.
Eigen::Vector< zono_float, -1 >	optimize_over (const Eigen::SparseMatrix< zono_float > &P, const Eigen::Vector< zono_float, -1 > &q, zono_float c=0, const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr) const
	Solves optimization problem with quadratic objective over the current set.
Eigen::Vector< zono_float, -1 >	project_point (const Eigen::Vector< zono_float, -1 > &x, const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr) const
	Returns the projection of the point x onto the set object.
bool	is_empty (const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr) const
	Returns true if the set is provably empty, false otherwise.
zono_float	support (const Eigen::Vector< zono_float, -1 > &d, const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr)
	Computes support function of the set in the direction d.
bool	contains_point (const Eigen::Vector< zono_float, -1 > &x, const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr) const
	Checks whether the point x is contained in the set object.
Box	bounding_box (const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr)
	Computes a bounding box of the set object as a Box object.
std::vector< ConZono >	get_leaves (bool remove_redundancy=true, const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr, int n_leaves=std::numeric_limits< int >::max(), int contractor_iter=10) const
	Computes individual constrained zonotopes whose union is the hybrid zonotope object.

Protected Member Functions
virtual Eigen::Vector< zono_float, -1 >	do_optimize_over (const Eigen::SparseMatrix< zono_float > &P, const Eigen::Vector< zono_float, -1 > &q, zono_float c, const OptSettings &settings, OptSolution *solution) const
virtual Eigen::Vector< zono_float, -1 >	do_project_point (const Eigen::Vector< zono_float, -1 > &x, const OptSettings &settings, OptSolution *solution) const
virtual bool	do_is_empty (const OptSettings &settings, OptSolution *solution) const
virtual zono_float	do_support (const Eigen::Vector< zono_float, -1 > &d, const OptSettings &settings, OptSolution *solution)
virtual bool	do_contains_point (const Eigen::Vector< zono_float, -1 > &x, const OptSettings &settings, OptSolution *solution) const
virtual Box	do_bounding_box (const OptSettings &settings, OptSolution *solution)
virtual std::unique_ptr< HybZono >	do_complement (zono_float, bool remove_redundancy, const OptSettings &settings, OptSolution *solution, int n_leaves, int contractor_iter)
OptSolution	mi_opt (const Eigen::SparseMatrix< zono_float > &P, const Eigen::Vector< zono_float, -1 > &q, zono_float c, const Eigen::SparseMatrix< zono_float > &A, const Eigen::Vector< zono_float, -1 > &b, const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr) const
std::vector< OptSolution >	mi_opt_multisol (const Eigen::SparseMatrix< zono_float > &P, const Eigen::Vector< zono_float, -1 > &q, zono_float c, const Eigen::SparseMatrix< zono_float > &A, const Eigen::Vector< zono_float, -1 > &b, int n_sols, const OptSettings &settings=OptSettings(), OptSolution *solution=nullptr) const

Static Protected Member Functions
static void	remove_generators (Eigen::SparseMatrix< zono_float > &G, Eigen::SparseMatrix< zono_float > &A, const std::set< int > &idx_to_remove)
static std::set< int >	find_unused_generators (const Eigen::SparseMatrix< zono_float > &G, const Eigen::SparseMatrix< zono_float > &A)

Protected Attributes
Eigen::SparseMatrix< zono_float >	G = Eigen::SparseMatrix<zono_float>(0, 0)
	generator matrix G = [Gc, Gb]
Eigen::SparseMatrix< zono_float >	Gc = Eigen::SparseMatrix<zono_float>(0, 0)
	continuous generator matrix
Eigen::SparseMatrix< zono_float >	Gb = Eigen::SparseMatrix<zono_float>(0, 0)
	binary generator matrix
Eigen::SparseMatrix< zono_float >	A = Eigen::SparseMatrix<zono_float>(0, 0)
	constraint matrix A = [Ac, Ab]
Eigen::SparseMatrix< zono_float >	Ac = Eigen::SparseMatrix<zono_float>(0, 0)
	continuous constraint matrix
Eigen::SparseMatrix< zono_float >	Ab = Eigen::SparseMatrix<zono_float>(0, 0)
	binary constraint matrix
Eigen::Vector< zono_float, -1 >	c = Eigen::Vector<zono_float, -1>(0)
	center vector
Eigen::Vector< zono_float, -1 >	b = Eigen::Vector<zono_float, -1>(0)
	constraint vector
int	n = 0
	set dimension
int	nG = 0
	total number of factors. nG = nGc + nGb
int	nGc = 0
	number of continuous factors
int	nGb = 0
	number of binary factors
int	nC = 0
	number of constraints
bool	zero_one_form = false
	flag to indicate whether the set is in 0-1 or -1-1 form
bool	sharp = false
	flag to indicate whether the set is known to be sharp (i.e., convex relaxation = convex hull)

Friends
std::ostream &	operator<< (std::ostream &os, const HybZono &Z)
	Displays set information to the given output stream.
std::unique_ptr< HybZono >	affine_map (const HybZono &Z, const Eigen::SparseMatrix< zono_float > &R, const Eigen::Vector< zono_float, -1 > &s)
	Returns affine map R*Z + s of set Z.
std::unique_ptr< HybZono >	project_onto_dims (const HybZono &Z, const std::vector< int > &dims)
	Projects set Z onto the dimensions specified in dims.
std::unique_ptr< HybZono >	minkowski_sum (const HybZono &Z1, HybZono &Z2)
	Computes Minkowski sum of two sets Z1 and Z2.
std::unique_ptr< HybZono >	pontry_diff (HybZono &Z1, HybZono &Z2, bool exact)
	Computes the Pontryagin difference Z1 - Z2.
std::unique_ptr< HybZono >	intersection (const HybZono &Z1, HybZono &Z2, const Eigen::SparseMatrix< zono_float > &R)
	Computes the generalized intersection of sets Z1 and Z2 over the matrix R.
std::unique_ptr< HybZono >	intersection_over_dims (const HybZono &Z1, HybZono &Z2, const std::vector< int > &dims)
	Computes the generalized intersection of sets Z1 and Z2 over the specified dimensions.
std::unique_ptr< HybZono >	halfspace_intersection (HybZono &Z, const Eigen::SparseMatrix< zono_float > &H, const Eigen::Vector< zono_float, -1 > &f, const Eigen::SparseMatrix< zono_float > &R)
	Computes the intersection generalized intersection of set Z with halfspace H*x <= f over matrix R.
std::unique_ptr< HybZono >	union_of_many (const std::vector< std::shared_ptr< HybZono > > &Zs, bool preserve_sharpness, bool expose_indicators)
	Computes union of several sets.
std::unique_ptr< HybZono >	cartesian_product (const HybZono &Z1, HybZono &Z2)
	Computes the Cartesian product of two sets Z1 and Z2.
std::unique_ptr< HybZono >	constrain (HybZono &Z, const std::vector< Inequality > &ineqs, const Eigen::SparseMatrix< zono_float > &R)
	Applies inequalities to set.
std::unique_ptr< HybZono >	set_diff (const HybZono &Z1, HybZono &Z2, zono_float delta_m, bool remove_redundancy, const OptSettings &settings, OptSolution *solution, int n_leaves, int contractor_iter)
	Set difference Z1 \ Z2.
std::unique_ptr< HybZono >	vrep_2_hybzono (const std::vector< Eigen::Matrix< zono_float, -1, -1 > > &Vpolys, bool expose_indicators)
	Computes a hybrid zonotope from a union of vertex representation polytopes.
std::unique_ptr< HybZono >	zono_union_2_hybzono (std::vector< Zono > &Zs, bool expose_indicators)
	Computes a hybrid zonotope from a union of zonotopes.

Detailed Description

Hybrid zonotope class.

A hybrid zonotope is defined as: Z = {Gc * xi_c + Gb * xi_b + c | Ac * xi_c + Ab * xi_b = b, xi_c in [-1, 1]^nGc, xi_b in {-1, 1}^nGb}. Equivalently, the following shorthand can be used: Z = <Gc, Gb, c, Ac, Ab, b>. Optionally, in 0-1 form, the factors are xi_c in [0, 1]^nGc, xi_b in {0, 1}^nGb. The set dimension is n, and the number of equality constraints is nC.

Constructor & Destructor Documentation

HybZono() [1/2]

ZonoOpt::HybZono::HybZono ( )

default

Default constructor for HybZono class.

HybZono() [2/2]

ZonoOpt::HybZono::HybZono	(	const Eigen::SparseMatrix< zono_float > &	Gc,
		const Eigen::SparseMatrix< zono_float > &	Gb,
		const Eigen::Vector< zono_float, -1 > &	c,
		const Eigen::SparseMatrix< zono_float > &	Ac,
		const Eigen::SparseMatrix< zono_float > &	Ab,
		const Eigen::Vector< zono_float, -1 > &	b,
		bool	zero_one_form = false,
		bool	sharp = false
	)

HybZono constructor.

Parameters

Gc	continuous generator matrix
Gb	binary generator matrix
c	center
Ac	continuous constraint matrix
Ab	binary constraint matrix
b	constraint vector
zero_one_form	true if set is in 0-1 form
sharp	true if set is known to be sharp, i.e., convex relaxation = convex hull

~HybZono()

virtual ZonoOpt::HybZono::~HybZono ( )

virtualdefault

Member Function Documentation

bounding_box()

Box ZonoOpt::HybZono::bounding_box ( const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr  )

inline

Computes a bounding box of the set object as a Box object.

Parameters

settings	optimization settings structure
solution	optimization solution structure pointer, populated with result

Returns

Box Z_bb

In general, solves 2*n support optimizations where n is the set dimension to compute a bounding box.

clone()

HybZono * ZonoOpt::HybZono::clone ( ) const

virtual

Clone method for polymorphic behavior.

Reimplemented in ZonoOpt::ConZono, ZonoOpt::EmptySet, ZonoOpt::Point, and ZonoOpt::Zono.

complement()

virtual std::unique_ptr< HybZono > ZonoOpt::HybZono::complement ( const zono_float  delta_m = 100, const bool  remove_redundancy = true, const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr, const int  n_leaves = std::numeric_limits<int>::max(), const int  contractor_iter = 100  )

inlinevirtual

Computes the complement of the set Z.

Parameters

delta_m	parameter defining range of complement
remove_redundancy	remove redundant constraints and unused generators in get_leaves function call
settings	optimization settings for get_leaves function call
solution	optimization solution for get_leaves function call
n_leaves	maximum number of leaves to return in get_leaves function call
contractor_iter	number of interval contractor iterations in remove_redundancy if using

Returns

Hybrid zonotope complement of the given set

Computes the complement according to the method of Bird and Jain: "Unions and Complements of Hybrid Zonotopes" delta_m is a parameter that defines the set over which the complement is defined. For a constrained zonotope, the complement is restricted to the set X = {G \xi + c | A \xi = b, \xi \in [-1-delta_m, 1+delta+m]^{nG}}.

contains_point()

bool ZonoOpt::HybZono::contains_point ( const Eigen::Vector< zono_float, -1 > &  x, const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr  ) const

inline

Checks whether the point x is contained in the set object.

Parameters

x	point to be checked for set containment
settings	optimization settings structure
solution	optimization solution structure pointer, populated with result

False positives are possible; will return true if the optimization converges within the specified tolerances. Will return false only if an infeasibility certificate is found, i.e., false negatives are not possible.

convert_form()

void ZonoOpt::HybZono::convert_form ( )

virtual

Converts the set representation between -1-1 and 0-1 forms.

This method converts the set representation between -1-1 and 0-1 forms. If the set is in -1-1 form, then xi_c in [-1,1] and xi_b in {-1,1}. If the set is in 0-1 form, then xi_c in [0,1] and xi_b in {0,1}.

Reimplemented in ZonoOpt::ConZono, ZonoOpt::Point, and ZonoOpt::Zono.

convex_relaxation()

std::unique_ptr< ConZono > ZonoOpt::HybZono::convex_relaxation ( ) const

virtual

Returns convex relaxation of the hybrid zonotope.

Returns

Constrained zonotope Z = <[Gc, Gb], c, [Ac, Ab,], b>

This method returns the convex relaxation of the hybrid zonotope. If the set is sharp, the convex relaxation is the convex hull.

do_bounding_box()

Box ZonoOpt::HybZono::do_bounding_box ( const OptSettings &  settings, OptSolution *  solution  )

protectedvirtual

Reimplemented in ZonoOpt::EmptySet, ZonoOpt::Point, ZonoOpt::Zono, and ZonoOpt::ConZono.

do_complement()

std::unique_ptr< HybZono > ZonoOpt::HybZono::do_complement ( zono_float  delta_m, bool  remove_redundancy, const OptSettings &  settings, OptSolution *  solution, int  n_leaves, int  contractor_iter  )

protectedvirtual

Reimplemented in ZonoOpt::ConZono, and ZonoOpt::EmptySet.

do_contains_point()

bool ZonoOpt::HybZono::do_contains_point ( const Eigen::Vector< zono_float, -1 > &  x, const OptSettings &  settings, OptSolution *  solution  ) const

protectedvirtual

Reimplemented in ZonoOpt::EmptySet, ZonoOpt::Point, and ZonoOpt::ConZono.

do_is_empty()

bool ZonoOpt::HybZono::do_is_empty ( const OptSettings &  settings, OptSolution *  solution  ) const

protectedvirtual

Reimplemented in ZonoOpt::EmptySet, ZonoOpt::Zono, and ZonoOpt::ConZono.

do_optimize_over()

Eigen::Vector< zono_float, -1 > ZonoOpt::HybZono::do_optimize_over ( const Eigen::SparseMatrix< zono_float > &  P, const Eigen::Vector< zono_float, -1 > &  q, zono_float  c, const OptSettings &  settings, OptSolution *  solution  ) const

protectedvirtual

Reimplemented in ZonoOpt::Point, ZonoOpt::EmptySet, and ZonoOpt::ConZono.

do_project_point()

Eigen::Vector< zono_float, -1 > ZonoOpt::HybZono::do_project_point ( const Eigen::Vector< zono_float, -1 > &  x, const OptSettings &  settings, OptSolution *  solution  ) const

protectedvirtual

Reimplemented in ZonoOpt::EmptySet, ZonoOpt::Point, and ZonoOpt::ConZono.

do_support()

zono_float ZonoOpt::HybZono::do_support ( const Eigen::Vector< zono_float, -1 > &  d, const OptSettings &  settings, OptSolution *  solution  )

protectedvirtual

Reimplemented in ZonoOpt::EmptySet, ZonoOpt::Point, ZonoOpt::Zono, and ZonoOpt::ConZono.

find_unused_generators()

std::set< int > ZonoOpt::HybZono::find_unused_generators ( const Eigen::SparseMatrix< zono_float > &  G, const Eigen::SparseMatrix< zono_float > &  A  )

staticprotected

get_A()

virtual Eigen::SparseMatrix< zono_float > ZonoOpt::HybZono::get_A ( ) const

inlinevirtual

Returns constraint matrix.

Returns

A

get_Ab()

virtual Eigen::SparseMatrix< zono_float > ZonoOpt::HybZono::get_Ab ( ) const

inlinevirtual

Returns binary constraint matrix.

Returns

Ab

get_Ac()

virtual Eigen::SparseMatrix< zono_float > ZonoOpt::HybZono::get_Ac ( ) const

inlinevirtual

Returns continuous constraint matrix.

Returns

Ac

get_b()

virtual Eigen::Vector< zono_float, -1 > ZonoOpt::HybZono::get_b ( ) const

inlinevirtual

Returns constraint vector.

Returns

b

get_c()

virtual Eigen::Vector< zono_float, -1 > ZonoOpt::HybZono::get_c ( ) const

inlinevirtual

Returns center vector.

Returns

c

get_G()

virtual Eigen::SparseMatrix< zono_float > ZonoOpt::HybZono::get_G ( ) const

inlinevirtual

Returns generator matrix.

Returns

G

get_Gb()

virtual Eigen::SparseMatrix< zono_float > ZonoOpt::HybZono::get_Gb ( ) const

inlinevirtual

Returns binary generator matrix.

Returns

Gb

get_Gc()

virtual Eigen::SparseMatrix< zono_float > ZonoOpt::HybZono::get_Gc ( ) const

inlinevirtual

Returns continuous generator matrix.

Returns

Gc

get_leaves()

std::vector< ConZono > ZonoOpt::HybZono::get_leaves	(	bool	remove_redundancy = true,
		const OptSettings &	settings = OptSettings(),
		OptSolution *	solution = nullptr,
		int	n_leaves = std::numeric_limits<int>::max(),
		int	contractor_iter = 10
	)		const

Computes individual constrained zonotopes whose union is the hybrid zonotope object.

Parameters

remove_redundancy	flag to make call to remove_redundancy for each identified leaf
settings	optimization settings structure
solution	optimization solution structure pointer, populated with result
n_leaves	max number of leaves to find
contractor_iter	number of interval contractor iterations to run if using remove_redundancy

Returns

vector of constrained zonotopes [Z0, Z1, ...] such that Zi is a subset of the current set for all i

Searches for constrained zonotopes that correspond to feasible combinations of the hybrid zonotope binary variables. If the branch and bound converges (i.e., did not hit max time, max number of branch and bound iterations, or max nodes in queue) and the n_leaves argument does not stop the optimization before exhausting all possibilities, then the resulting vector of constrained zonotopes can be unioned to recover the original set. It is possible for a leaf to be the empty set if the optimization converges before detecting an infeasibility certificate.

get_n()

virtual int ZonoOpt::HybZono::get_n ( ) const

inlinevirtual

Returns dimension of set.

Returns

n

get_nC()

virtual int ZonoOpt::HybZono::get_nC ( ) const

inlinevirtual

Returns number of constraints in set definition.

Returns

nC

get_nG()

virtual int ZonoOpt::HybZono::get_nG ( ) const

inlinevirtual

Returns number of generators in set definition.

Returns

nG

get_nGb()

virtual int ZonoOpt::HybZono::get_nGb ( ) const

inlinevirtual

Returns number of binary generators in set definition.

Returns

nGb

get_nGc()

virtual int ZonoOpt::HybZono::get_nGc ( ) const

inlinevirtual

Returns number of continuous generators in set definition.

Returns

nGc

is_0_1_form()

virtual bool ZonoOpt::HybZono::is_0_1_form ( ) const

inlinevirtual

Returns true if factors are in range [0,1], false if they are in range [-1,1].

Returns

zero_one_form flag

is_conzono()

bool ZonoOpt::HybZono::is_conzono

(

)

const

Polymorphic type checking: true if set is a constrained zonotope.

is_empty()

bool ZonoOpt::HybZono::is_empty ( const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr  ) const

inline

Returns true if the set is provably empty, false otherwise.

Parameters

settings	optimization settings structure
solution	optimization solution structure pointer, populated with result

Returns

flag indicating whether set is provably empty

is_empty_set()

bool ZonoOpt::HybZono::is_empty_set

(

)

const

Polymorphic type checking: true if set is empty set object.

is_hybzono()

bool ZonoOpt::HybZono::is_hybzono

(

)

const

Polymorphic type checking: true if set is a hybrid zonotope.

is_point()

bool ZonoOpt::HybZono::is_point

(

)

const

Polymorphic type checking: true if set is a point.

is_sharp()

bool ZonoOpt::HybZono::is_sharp ( ) const

inline

Returns true if set is known to be sharp.

Returns

sharp flag

A set is sharp if its convex relaxation is equal to its convex hull.

is_zono()

bool ZonoOpt::HybZono::is_zono

(

)

const

Polymorphic type checking: true if set is a zonotope.

mi_opt()

OptSolution ZonoOpt::HybZono::mi_opt ( const Eigen::SparseMatrix< zono_float > &  P, const Eigen::Vector< zono_float, -1 > &  q, zono_float  c, const Eigen::SparseMatrix< zono_float > &  A, const Eigen::Vector< zono_float, -1 > &  b, const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr  ) const

protected

mi_opt_multisol()

std::vector< OptSolution > ZonoOpt::HybZono::mi_opt_multisol ( const Eigen::SparseMatrix< zono_float > &  P, const Eigen::Vector< zono_float, -1 > &  q, zono_float  c, const Eigen::SparseMatrix< zono_float > &  A, const Eigen::Vector< zono_float, -1 > &  b, int  n_sols, const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr  ) const

protected

optimize_over()

Eigen::Vector< zono_float, -1 > ZonoOpt::HybZono::optimize_over ( const Eigen::SparseMatrix< zono_float > &  P, const Eigen::Vector< zono_float, -1 > &  q, zono_float  c = 0, const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr  ) const

inline

Solves optimization problem with quadratic objective over the current set.

Parameters

P	quadratic objective matrix
q	linear objective vector
c	constant term in objective function
settings	optimization settings structure
solution	optimization solution structure pointer, populated with result

Returns

point z in the current set

Solves optimization problem of the form min 0.5*z^T*P*z + q^T*z + c where z is a vector in the current set

print()

std::string ZonoOpt::HybZono::print ( ) const

virtual

Returns set information as a string.

Reimplemented in ZonoOpt::ConZono, ZonoOpt::EmptySet, ZonoOpt::Point, and ZonoOpt::Zono.

project_point()

Eigen::Vector< zono_float, -1 > ZonoOpt::HybZono::project_point ( const Eigen::Vector< zono_float, -1 > &  x, const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr  ) const

inline

Returns the projection of the point x onto the set object.

Parameters

x	point to be projected
settings	optimization settings structure
solution	optimization solution structure pointer, populated with result

Returns

point z in the current set

remove_generators()

void ZonoOpt::HybZono::remove_generators ( Eigen::SparseMatrix< zono_float > &  G, Eigen::SparseMatrix< zono_float > &  A, const std::set< int > &  idx_to_remove  )

staticprotected

remove_redundancy()

void ZonoOpt::HybZono::remove_redundancy ( int  contractor_iter = 100 )

virtual

Removes redundant constraints and any unused generators.

Parameters

contractor_iter

number of interval contractor iterations to run

This method uses an interval contractor to detect generators that can be removed. Additionally, any linearly dependent rows of the constraint matrix A are removed. If the linearly dependent constraints are not consistent (e.g., if A = [1, 0.1; 1, 0.1] and b = [1; 0.8]), the returned set is not equivalent to the original set. Unused factors are also removed.

Reimplemented in ZonoOpt::Point.

set()

void ZonoOpt::HybZono::set	(	const Eigen::SparseMatrix< zono_float > &	Gc,
		const Eigen::SparseMatrix< zono_float > &	Gb,
		const Eigen::Vector< zono_float, -1 > &	c,
		const Eigen::SparseMatrix< zono_float > &	Ac,
		const Eigen::SparseMatrix< zono_float > &	Ab,
		const Eigen::Vector< zono_float, -1 > &	b,
		bool	zero_one_form = false,
		bool	sharp = false
	)

Reset hybrid zonotope object with the given parameters.

Parameters

Gc	continuous generator matrix
Gb	binary generator matrix
c	center
Ac	continuous constraint matrix
Ab	binary constraint matrix
b	constraint vector
zero_one_form	true if set is in 0-1 form
sharp	true if set is known to be sharp, i.e., convex relaxation = convex hull

support()

zono_float ZonoOpt::HybZono::support ( const Eigen::Vector< zono_float, -1 > &  d, const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr  )

inline

Computes support function of the set in the direction d.

Parameters

d	vector defining direction for support function
settings	optimization settings structure
solution	optimization solution structure pointer, populated with result

Returns

support

Solves max_{z in Z} <z, d> where <., .> is the inner product

Friends And Related Symbol Documentation

affine_map

std::unique_ptr< HybZono > affine_map ( const HybZono &  Z, const Eigen::SparseMatrix< zono_float > &  R, const Eigen::Vector< zono_float, -1 > &  s = Eigen::Vector<zono_float, -1>()  )

friend

Returns affine map R*Z + s of set Z.

Parameters

Z	zonotopic set
R	affine map matrix
s	vector offset

Returns

zonotopic set

cartesian_product

std::unique_ptr< HybZono > cartesian_product ( const HybZono &  Z1, HybZono &  Z2  )

friend

Computes the Cartesian product of two sets Z1 and Z2.

Parameters

Z1	zonotopic set
Z2	zonotopic set

Returns

zonotopic set

constrain

std::unique_ptr< HybZono > constrain ( HybZono &  Z, const std::vector< Inequality > &  ineqs, const Eigen::SparseMatrix< zono_float > &  R = Eigen::SparseMatrix<zono_float>()  )

friend

Applies inequalities to set.

Parameters

Z	Set for inequalities to be applied to.
ineqs	Vector of inequalities.
R	For generalized intersection with the inequalities. Defaults to identity.

Returns

zonotopic set

Constrains set Z by applying the given inequalities to the set. For example, given a set Z with states z0, z1, z2, the constraint z0 + z1 - z2 <= 2 could be added via an inequality object. R is used for generalized intersection-like operations. For instance, when all the inequalities are <= inequalities, this function returns Z int_R (Hx<=f) where H is the halfspace represented by the inequalities.

halfspace_intersection

std::unique_ptr< HybZono > halfspace_intersection ( HybZono &  Z, const Eigen::SparseMatrix< zono_float > &  H, const Eigen::Vector< zono_float, -1 > &  f, const Eigen::SparseMatrix< zono_float > &  R = Eigen::SparseMatrix<zono_float>()  )

friend

Computes the intersection generalized intersection of set Z with halfspace H*x <= f over matrix R.

Parameters

Z	zonotopic set
H	halfspace matrix
f	halfspace vector
R	affine map matrix

Returns

zonotopic set

intersection

std::unique_ptr< HybZono > intersection ( const HybZono &  Z1, HybZono &  Z2, const Eigen::SparseMatrix< zono_float > &  R = Eigen::SparseMatrix<zono_float>()  )

friend

Computes the generalized intersection of sets Z1 and Z2 over the matrix R.

Parameters

Z1	zonotopic set
Z2	zonotopic set
R	affine map matrix

Returns

zonotopic set

intersection_over_dims

std::unique_ptr< HybZono > intersection_over_dims ( const HybZono &  Z1, HybZono &  Z2, const std::vector< int > &  dims  )

friend

Computes the generalized intersection of sets Z1 and Z2 over the specified dimensions.

Parameters

Z1	zonotopic set
Z2	zonotopic set
dims	vector of dimensions

Returns

zonotopic set

minkowski_sum

std::unique_ptr< HybZono > minkowski_sum ( const HybZono &  Z1, HybZono &  Z2  )

friend

Computes Minkowski sum of two sets Z1 and Z2.

Parameters

Z1	zonotopic set
Z2	zonotopic set

Returns

zonotopic set

operator<<

std::ostream & operator<< ( std::ostream &  os, const HybZono &  Z  )

friend

Displays set information to the given output stream.

Parameters

os
Z

pontry_diff

std::unique_ptr< HybZono > pontry_diff ( HybZono &  Z1, HybZono &  Z2, bool  exact = false  )

friend

Computes the Pontryagin difference Z1 - Z2.

Parameters

Z1	minuend
Z2	subtrahend
exact	require output to be exact, otherwise inner approximation will be returned

Returns

zonotopic set

For inner approximations (exact = false), the algorithm from Vinod et. al. 2025 is used. Note that this algorithm is exact when the minuend is a constrained zonotope and the matrix [G;A] is invertible. Exact Pontryagin difference can only be computed when the subtrahend is a zonotope. If subtrahend is a constrained zonotope, it will first be over-approximated as a zonotope. If subtrahend is a hybrid zonotope, a get_leaves operation will first be performed to produce a union of constrained zonotopes. If the minuend is a hybrid zonotope and exact is false, a get_leaves operation will be performed for Z1 to reduce the number of leaves in the resulting set.

project_onto_dims

std::unique_ptr< HybZono > project_onto_dims ( const HybZono &  Z, const std::vector< int > &  dims  )

friend

Projects set Z onto the dimensions specified in dims.

Parameters

Z	zonotopic set
dims	vector of dimensions

Returns

zonotopic set

set_diff

std::unique_ptr< HybZono > set_diff ( const HybZono &  Z1, HybZono &  Z2, zono_float  delta_m = 100, bool  remove_redundancy = true, const OptSettings &  settings = OptSettings(), OptSolution *  solution = nullptr, int  n_leaves = std::numeric_limits<int>::max(), int  contractor_iter = 100  )

friend

Set difference Z1 \ Z2.

Parameters

Z1	zonotopic set
Z2	zonotopic set
delta_m	parameter defining range of complement
remove_redundancy	remove redundant constraints and unused generators in get_leaves function call
settings	optimization settings for get_leaves function call
solution	optimization solution for get_leaves function call
n_leaves	maximum number of leaves to return in get_leaves function call
contractor_iter	number of interval contractor iterations to run if using remove_redundancy

Returns

zonotopic set

union_of_many

std::unique_ptr< HybZono > union_of_many ( const std::vector< std::shared_ptr< HybZono > > &  Zs, bool  preserve_sharpness = false, bool  expose_indicators = false  )

friend

Computes union of several sets.

Parameters

Zs	Sets to be unioned.
preserve_sharpness	Flag to preserve sharpness of the union at expense of complexity.
expose_indicators	Flag to append indicator set to the union.

Returns

zonotopic set

Computes union of sets {Z0, Z1, ..., Zn}. If expose_indicators is true, returns union({Z0, ..., Zn}) x I where I is the indicator set for the union. Specifically, each dimension of I corresponds to one of the Zi in the union. So for union_of_many({Z0, Z1, Z2}, true) with Z0, Z1, Z2 not intersecting, if a vector [z, i] is in union({Z0, Z1, Z2}) x I, then i = [1, 0, 0] if z is in Z0, etc.

vrep_2_hybzono

std::unique_ptr< HybZono > vrep_2_hybzono ( const std::vector< Eigen::Matrix< zono_float, -1, -1 > > &  Vpolys, bool  expose_indicators = false  )

friend

Computes a hybrid zonotope from a union of vertex representation polytopes.

Parameters

Vpolys	V-rep polytopes to be unioned.
expose_indicators	Flag to append indicator set to the union.

Returns

zonotopic set

Vpolys is a vector of matrices, where each matrix represents a polytope in vertex representation. Each row in each polytope matrix is a vertex of the polytope, and each column corresponds to a dimension. The function constructs a hybrid zonotope in [0,1] form that represents the union of these polytopes. This function computes union of sets {V0, V1, ..., Vn}. If expose_indicators is true, returns union({V0, ..., Vn}) x I where I is the indicator set for the union. Specifically, each dimension of I corresponds to one of the Vi in the union. So for vrep_2_hybzono({V0, V1, V2}, true) with V0, V1, V2 not intersecting, if a vector [z, i] is in union({V0, V1, V2}) x I, then i = [1, 0, 0] if z is in V0, etc.

zono_union_2_hybzono

std::unique_ptr< HybZono > zono_union_2_hybzono ( std::vector< Zono > &  Zs, bool  expose_indicators = false  )

friend

Computes a hybrid zonotope from a union of zonotopes.

Parameters

Zs	A vector of zonotopes to be unioned.
expose_indicators	Flag to append indicator set to the union.

Returns

zonotopic set

This function computes union of sets {Z0, Z1, ..., Zn}. This can be more efficient than union_of_many if all sets are zonotopes because generators can be reused. If expose_indicators is true, returns union({Z0, ..., Zn}) x I where I is the indicator set for the union. Specifically, each dimension of I corresponds to one of the Zi in the union. So for zono_union_2_hybzono({Z0, Z1, Z2}, true) with Z0, Z1, VZ2 not intersecting, if a vector [z, i] is in union({Z0, Z1, Z2}) x I, then i = [1, 0, 0] if z is in Z0, etc.

Member Data Documentation

A

Eigen::SparseMatrix<zono_float> ZonoOpt::HybZono::A = Eigen::SparseMatrix<zono_float>(0, 0)

protected

constraint matrix A = [Ac, Ab]

Ab

Eigen::SparseMatrix<zono_float> ZonoOpt::HybZono::Ab = Eigen::SparseMatrix<zono_float>(0, 0)

protected

binary constraint matrix

Ac

Eigen::SparseMatrix<zono_float> ZonoOpt::HybZono::Ac = Eigen::SparseMatrix<zono_float>(0, 0)

protected

continuous constraint matrix

b

Eigen::Vector<zono_float, -1> ZonoOpt::HybZono::b = Eigen::Vector<zono_float, -1>(0)

protected

constraint vector

c

Eigen::Vector<zono_float, -1> ZonoOpt::HybZono::c = Eigen::Vector<zono_float, -1>(0)

protected

center vector

G

Eigen::SparseMatrix<zono_float> ZonoOpt::HybZono::G = Eigen::SparseMatrix<zono_float>(0, 0)

protected

generator matrix G = [Gc, Gb]

Gb

Eigen::SparseMatrix<zono_float> ZonoOpt::HybZono::Gb = Eigen::SparseMatrix<zono_float>(0, 0)

protected

binary generator matrix

Gc

Eigen::SparseMatrix<zono_float> ZonoOpt::HybZono::Gc = Eigen::SparseMatrix<zono_float>(0, 0)

protected

continuous generator matrix

n

int ZonoOpt::HybZono::n = 0

protected

set dimension

nC

int ZonoOpt::HybZono::nC = 0

protected

number of constraints

nG

int ZonoOpt::HybZono::nG = 0

protected

total number of factors. nG = nGc + nGb

nGb

int ZonoOpt::HybZono::nGb = 0

protected

number of binary factors

nGc

int ZonoOpt::HybZono::nGc = 0

protected

number of continuous factors

sharp

bool ZonoOpt::HybZono::sharp = false

protected

flag to indicate whether the set is known to be sharp (i.e., convex relaxation = convex hull)

zero_one_form

bool ZonoOpt::HybZono::zero_one_form = false

protected

flag to indicate whether the set is in 0-1 or -1-1 form

---

The documentation for this class was generated from the following files:

• /home/joshr/Documents/Projects/ZonoOpt/include/zonoopt/HybZono.hpp
• /home/joshr/Documents/Projects/ZonoOpt/src/HybZono.cpp
• /home/joshr/Documents/Projects/ZonoOpt/src/PolymorphicFunctions.cpp